|
scientific, peer reviewed paper (not) presented at the Engineering Mechanics Institute August 2013 conference at Evanston, IL, USA, by |
|
|
|
The theme of the 2013 Engineering Mechanics Institute conference was "Mechanics for Sustainable and Resilient Infrastructures" and the program was a forum where engineers and mechanicians contribute their expertise to one of the most pressing questions of our society: How can we make the nation's infrastructures safer, more durable, more affordable, and more environmentally friendly during their entire lifetime? Professor Gianluca Cusatis and his secretary Ms. Jennie Edelstein of the Department of Civil and Environmental Engineering of the Northwestern University, Tech Building Room A236, 2145 North Sheridan Road, Evanston, IL 60208-3109, Telephone: (847) 467-2673 had been kind enough to invite me to present the below scientific paper, peer reviewed and accepted by the EMI staff at Evanston 5-7 August, 2013. The presentation was supposed to take place on August 7 at 10.15 am - 12.15 pm at 206 Arch Room of the Norris Center of the Northwestern University (Session 5.7). Karen Chou, Assistant Chair of Civil & Environmental Engineering and Clinical Professor of Civil & Environmental Engineering, Northwestern University, an expert of bolted connections in structures, and David Corr, Clinical Associate Professor of Civil and Environmental Engineering, Northwestern University, chaired the session. According the Civil & Environmental Engineering department of the Northwestern University, Evanston, IL, the weak top of a structure easily crushes the strong bottom of same structure by gravity and causes a progressive global collapse of the structure - a phenomenom used by terrorists. My paper demonstrates the folly of such ideas. The August 7 program could be down loaded from the web and also the abstract of and my full paper. This worked until July 27, 2013, when the program was changed. On July 28 at 22:35 hrs the following e-mail was received: Mr. Bjorkman:
Today 4 September 2021 all references to the EMI 2013 conference are removed from the Internet. The conference never took place!

At 8.45 am WTC 1 exploded up at the top close to the roof. It was later suggested a mysterious plane hit its north wall. At 9.03 am WTC 2 exploded at the top in a big fireball seen live on TV - another mysterious airplane hit its south wall, it was suggested! At 9.04 am WTC 6 exploded down at the ground and caught fire and NYFD started to extinguish it seen on many videos. At 9.35 am a mysterious airplane crashed into the Pentagon, Washington, DC, far away south we are told, and put it on fire. According a source two fire trucks arrived after 10 minutes at Pentagon and extinguished the fire but according Fake News media the fire lasted several days down at DC with plenty actors running around. Imagine, mysterious explosions took place both at NY and Washington, DC, at about the same time caused by mysterious planes that, some people suggest, never existed!! At 10.05 am WTC 2 collapsed from top in a fountain of smoke and dust. At 10.28 am WTC 1 also collapsed from top in a fountain of smoke and dust. At 5.20 pm WTC 7 collapsed from bottom up into a pile of floors stacked on top of each other.
Abstract: On September 11, 2001, the progressive, global, structural collapses of the man-made WTC 1 and 2 tower structures at NY were shown live on all five major TV channels in the USA. The structures could be seen to collapse from top down, when apparently the complete, loose, damaged by fire at lower end top part of each tower displaced down and crushed the part below by gravity producing fountains of debris, dust and broken parts with clouds of smoke shooting out upwards and sideways. The man-made structures were completely destroyed in less than 20 seconds and became dust and a heap or rubble that soon disappeared, shipped off to China. The collapses have been subject to some scientific papers suggesting that it is a natural hazard of some particular, man-made structure to suddenly collapse from top down by gravity when flying planes into the weak tops and that terrorists used the phenomenon. In this paper is described how the phenomenon progressive, global collapse from top down is physically impossible for any structure regardless of design, arrangements, materials used, etc. Reason is that a top assembly of elements of any structure cannot apply sufficient force and/or energy on the intact bottom assembly to destroy the latter. There is not enough stored energy available. Anyone suggesting something else or shows it 'live on TV' is a simple terrorist.
Anders Björkman, M.Sc., Heiwa Co, European Agency for Safety at Sea, Beausoleil, France
In several scientific, peer-reviewed papers published in the Journal of Engineering Mechanics, e.g. (1) "Closure to 'Mechanics of progressive collapse: Learning from World Trade Center and building demolitions' by Z. P. Bažant and Mathieu Verdure." Journal of Eng. Mech., 134(10), 917-923, Bažant, Z. P., and Verdure, M. (2007), (2) "Mechanics of progressive collapse: Learning from World Trade Center and building demolitions." Journal of Eng. Mech., 133, 308-319 and Bažant, Z. P., and Zhou, Y. (2002), (3) "Why did the World Trade Center collapse? Simple analysis." Journal of Eng. Mech., 128(1), 2-6, Bažant, Z. P., and Le, J.-L. (2008), etc, it is suggested, using a 1D-modeling approach, a line, and differential equations, that any man-made structure A can be destroyed or crushed down by its own top part C dropping on the structure A below by gravity. The top part C strangely becomes solid, while it crushes elements and joints of the structure below into dust and broken elements. The phenomenon is called progressive, global collapse. Wikipedia describes progressive collapse of a man-made structure as follows: "The collapse of the World Trade Center has been called "the most infamous paradigm" of progressive collapse. In the case of both towers, the top section tilted towards the face that had buckled, behaving largely as a solid block separate from the rest of the building. It fell at least one story in freefall and impacted the lower sections with a force equivalent to over thirty times its own weight. This was sufficient to buckle the columns of the story immediately below it; the block then fell freely through the distance of another story. Total collapse was now unavoidable as the process repeated through the entire height of the lower sections. The force of each impact was also much greater than the horizontal momentum of the section, which kept the tilt from increasing significantly before the falling reached the ground. It (the top part) remained intact throughout the collapse, with its center of gravity within the building's footprint. After crushing the lower section of the building, it was itself crushed when it hit the ground." Any attempts to correct the relevant Wikipedia article/definition are impossible! So the top C of the structure A becomes solid (?), it free falls, impacts, crushes the wall elements below, free falls again, impacts, crushes wall elements below, etc, etc, and nothing stops the solid top C until it hits … a heap of rubbish it has produced. Then the solid top C suddenly becomes rubbish. Is this science? (Somebody at Wikipedia has recently (August 7, 2013) removed above nonsense and now reports: "After a 3-year investigation by the National Institute of Standards and Technology, it was concluded that fire weakened the (top of the WTC) steel structure until the long bridge-like floor sections (called trusses) began to progressively sag. This sagging converted the downwards pull of the trusses into an inwards pull. This intensifying inwards pull on the walls eventually caused the outer columns of Tower 2, and later the inner columns of Tower 1, to buckle and fold, thus initiating the various progressive collapses". Maybe somebody read this paper censored by EMI but available on the Internet? April 26, 2015 Wikipedia proposes - "After a 3-year investigation by the National Institute of Standards and Technology, it was concluded that fire weakened the (top of the WTC) steel structure until the long bridge-like floor sections (called trusses) began to progressively sag. This sagging converted the downwards pull of the trusses into an inwards pull. This intensifying inwards pull on the walls eventually caused the outer columns of Tower 2, and later the inner columns of Tower 1, to buckle and fold, thus initiating the collapses." So now the various progressive collapses are just collapses and ... no explanation at all is given why some fire weakened floor trusses up top could cause the whole WTC towers to disintegrate in fountains of debris). Progressive collapse is illustrated in the figure below produced by Bažant, Z. P: The US National Institute of Standards and Technology, NIST, at Washington, DC, has adopted and confirmed the same idea in its 911-reports that are easily available on the Internet. According NIST the top part C applies energy on the bottom part A that the bottom part cannot absorb elastically and plastically and all load carrying elements and/or their connections in the structure fail. I call above unscientific nonsense the POUFF, POUFF theory illustrated in below figure and explained further down: 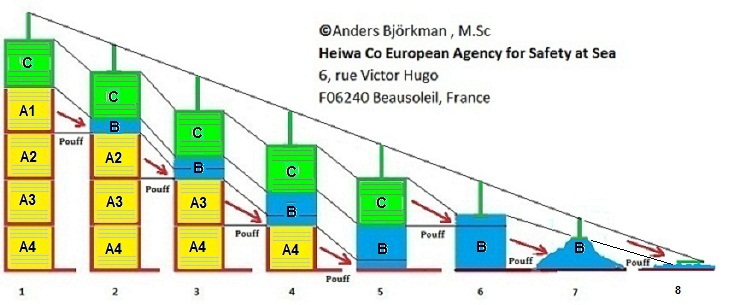 The top part C of any structure is originally carried by four parts A1, 2, 3 and 4 below one above the other of similar structure; even if lowest part A4 is four times stronger than A1 and five times stronger than top part C. A1 is just double as strong as C. Then top part C is given downward motion due to gravity (some supports between parts C and top A1 are buckled) and top part C applies, when impacting A1, released potential energy on the top part A1 that is crushed down into rubble B - POUFF - as top A1 cannot absorb the energy applied by C! The part A1 becomes smoke and dust or rubble B or whatever. It cannot really be seen due to the smoke and dust. Then the rubble B or the smoke (?) is accelerated by the top part C and gravity and more released potential energy is applied on the second part A2 that is crushed into more rubble B - another POUFF - as second part A2 cannot absorb the energy applied! The second part A2 becomes more smoke and dust or more B or whatever. It cannot be seen either. Smoke, you know! The crushing down will be repeated as many times as is required to crush parts A3 and A4 into more rubble B or smoke and dust. In this example the third and fourth parts A3 and A4 thus become smoke and dust or even more B or whatever. Then all A parts are rubble B because all A parts could not absorb the energy applied by top part C and rubble B! Then the rubble B crushes up top part C into more rubble B - the second final POUFF! The last POUFF is that B becomes a pyramid shaped heap of rubble. Bažant, Z. P has confirmed above nonsense several times in peer reviewed scientific papers! It cannot be demonstrated in a laboratory or on a building site - so you have to believe Bažant, Z. P. It is however very easy to demonstrate theoretically, numerically, in a laboratory and/or in real scale that any man- made structure A cannot globally collapse by itself from top down, when a small top part C of A drops on and impacts remainder of A by gravity from above. Reason is simply that such a man-made structure is always stronger at bottom than top. The hazard, risk or danger of global collapse from top down does not exist in the real world! This is good news. It will assist US authorities and learned societies like ASCE and EMI, Engineering Mechanics Institute, to improve safety against progressive collapse of structures everywhere without too much effort. The risk does not exist. I will explain it using a very simple model. A simple 2D model of any structure A structure is evidently three dimensional, 3D, but it can be represented in two dimensions, 2D, by a line or chain of connected elements, e.g. springs, at nodes that in turn are subject to forces acting on a mass of the node. The springs compress longitudinally and transversely, 2D. The findings evidently also apply in 3D. Let us therefore consider a tower structure of N floors (nodes), each of mass m, labeled from top (i=1) to bottom (i =N). · Adjacent floors (nodes) are separated by springs. All springs are weightless, have rest length L (m), and are perfectly elastic with constant stiffness k (N/m) until compressed longitudinally and laterally, 2D, a critical longitudinal displacement , when they compress plastically another displacement, after which they finally fail (and the length becomes 0). The springs represent the load carrying elements of the tower structure, e.g. external walls, pillars and interior columns. The tower structure is placed in a vacuum and fixed to a very large inertial mass, i.e. ground and subjected to a uniform gravitational field directed downwards. g = 9.82 m/s².
Static equilibrium The structure is in static equilibrium if Fn = nkx = nmg (N), x = mg/k. In static equilibrium the displacement x is everywhere the same and the same is true for the strain e =x/L and stress s (N/m² or Pa) in the spring. Safety factor The n springs below floor n can each support a load of FC = kxC before plastic deformation starts. If the actual design load of a spring is F, then the safety factor S = FC/F.
Elastic and plastic strain energy The work performed in compressing a spring elastically is E = kx²/2 (J). With x = 0.01L, which is typical for a pillar in a tower structure, a spring can elastically absorb ES = 0.00005kL² (J). If a spring is overloaded elastically and starts to deform plastically, the spring will develop plastic hinges which absorb more energy EP and which takes a certain time tP - and its effective length finally becomes 0 - it has broken! Let's assume that EP = ES. Actual values are easy to establish in a laboratory.
Numerical example Assume that the tower has N = 110 floors, each with mass m = 3.6 Mkg (i.e. 3 600 tons) and that L = 3.7 m. It means that the tower is 407 m tall, like WTC 1 or 2. The total number of springs in a tower of N floor is N(N+1)/2. Thus a tower with 110 floors consists of 6 105 springs. The top floor (or roof) is supported by 1 spring and the bottom floor is supported by 110 springs. The assembly of the 13 uppermost floors contains 91 springs, while the assembly of 97 lowest floors contains 6 014 springs. Let's call the assembly of the 13 uppermost floors top part C and let's remove the 13 bottom springs from C. Top part C then consists of 13 m connected by 78 springs (1 between top two m, 12 between lowest two m). The 78 springs in top part C can together absorb EC=78ES. Top part C weighs 48 800 tons. Let's call the assembly of the 97 lowest floors bottom part A. A's 110 lowest springs are connected to ground. The 6 014 springs in A can together absorb EA=6014ES. Bottom part A weighs 349 200 tons and is 7.2 times heavier than part C. If energy absorption is a measure of 'strength', A is 77.1 times 'stronger' than C.
Spring details - same everywhere Static force F in every spring is F = mg = 35.352 MN. The spring may have cross area of about 0.5 m², if it is of steel. The static stress in the spring is then about 70 MPa. Note that the static stress is same everywhere in every spring - at top and bottom of the structure. Let's assume S = 3, i.e. the springs will commence plastic deformation at 210 MPa stress. The material of the spring is steel. Note that the total cross area of removed springs below top part C is 6.5 m² (13 springs each 0.5 m²) and that the total cross area of springs at bottom of bottom part A is 55 m² (110 springs each 0.5 m²). The structure evidently gets 'stronger' with more springs added further down. The critical force FC of a spring is FC = 106.056 MN. After that it deforms plastically absorbing more energy and soon has length 0. Let's assume that spring stiffness k = 3 GN/m that is typical, when core and perimeter wall structure of WTC is replaced by one spring (a bundle of steel elements) with cross area 0.5 m² that can deform in 3-D. Actual k is easy to establish in a laboratory. Then xC = 0.037 m ES = k(xC)²/2 = 2.053 MJ x = 0.037/3 m E = kx²/2 = 0.228 MJ When the tower structure is in static equilibrium, each spring is compressed 0.037/3 m and 0.228MJ energy E is stored in it elastically. Our 110 floors structure is therefore elastically compressed 1.357 meters. However a spring can be compressed elastically to xC = 0.037 m (or 1% of L) before it starts to deform plastically and the energy EC required to compress it is then 2.053 MJ. From an energy absorption point of view factor of safety is 9 (actually static S²). All 6 105 springs in our structure can elastically absorb 12.53 GJ. Top part C can absorb elastically totally 78 x 2.053 = 160.1 MJ. Bottom part A can absorb elastically 6014 x 2.053 = 12.35 GJ. By dropping top part C a certain distance, e.g. L, a certain amount of potential energy ED is released, where ED = 13mLg = 1.7 GJ. It is 13.6% of what the tower itself can absorb elastically. By simple structural damage analysis you can establish whether top part C can damage A, ground or itself C.
Structural damage analysis experiment 1: Structure top part C collapses from bottom up In experiment 1 is described how something weak, top part C, dropped on rigid ground will be affected by the impact. The top part C assembly of 13 m is dropped on ground from distance L. At the impact C/ground total 1.7 GJ is applied to ground and C. The ground does not damp the impact. It is rigid or solid and can absorb plenty energy. Evidently top part C itself damps the impact - it becomes compressed and damaged: As top part C is 44.4 m tall and consists of 13 m separated by springs, it is the bottom floor m of C that physically contacts ground and is arrested by ground at the impact. The remaining 12 m above continue to displace down and compress the springs below. A certain damping takes place, when the springs compress elastically and plastically. As the dynamic forces acting on top part C and ground at impact and later are equal and opposite (the dynamic force is the energy applied (0.5ED ) divided by the displacement of the force - the structure is compressed and maybe damaged), it follows that top part C will absorb 0.5ED and rigid ground will also absorb 0.5ED in the impact. It would then appear that 0.85 GJ energy is applied on top part C one way or another and as top part C can only absorb 0.16 GJ elastically and 0.32 GJ plastically (or 0.48 GJ totally), all springs in top part C will fail. Ground is rigid and undamaged and can easily absorb 0.85 GJ. Top part C is, as seen, not very strong, and it is why its springs are 100% broken at impact with ground. In what order will the springs in top part C fail? It can be seen on videos of controlled demolitions of buildings, where the bottom supports are destroyed first and structure above drops and hits ground that destruction is from bottom up, thus: The bottom 12 springs fail first at impact with ground, 12 floors m above then drop down L, more potential energy is released, 11 springs fail at second impact, 11 m drop down L, 10 springs fail, 10 m drop, etc, etc, until the last one top spring fails and the last roof m impacts ground from L. Top part C, 12 L tall, is destroyed from bottom up in 12 steps that take a certain time. Total energy released due to failed springs after initial impact C/ground, i.e. when C is destroyed, is 72mLg or 8.82 GJ (it was stored in C prior impact) and all of it is absorbed by the ground. You can say that top part C is crushed-up by 13 impacts with solid ground. Bažant & Co suggest in their ridiculous, peer reviewed papers published in Journal of Engineering Mechanics that weak top part C is rigid and remains intact, when impacting, e.g. stronger bottom part A, and that is one false idea of Bažant later adopted by NIST as true.
Structural damage analysis experiment 2: Structure A loaded on top deforms elastically In experiment 2 is shown how bottom part A behaves, when statically loaded from above. Bottom part A is thus positioned on ground without C. A is, as already described, a tower structure of 97 m and 97 L tall. It consists of 6 014 springs that can absorb elastically totally 12.346 GJ. 1/9th of this energy is already stored statically in the tower so another 8/9th or 10.974 GJ can be applied and absorbed elastically. Considering plastic deformations another 10.974 GJ can be absorbed. The top floor m of A is supported by 14 springs located on the second floor m below that is supported by 15 springs further below, etc. The 14 top springs of bottom A can elastically absorb totally 28.74 MJ but are statically only loaded by one m. You can add another 13 m (i.e. C) on the 14 springs and then they are under original design load, like all the other springs in A. Thus, just adding 13 m on top of A nothing special will happen except that all springs in A are again under original design, static load. What happens if, in lieu of slowly putting 13 m on A we drop 13 m on A from L = 3.7 meter and we let 13 m impact A! Will the dynamic force at impact crush A?
Structural damage analysis experiment 3: Bottom part A, impacted on top, damps impact due to elastic and plastic deformations In experiment 3 is shown what happens, when a rigid mass of 13 m impacts A from above. 13 m are dropped on the top m of A from L = 3.7 m. The 13 m are connected together without any interconnecting springs, and that assembly is here called D. D is one rigid mass of 13 m. At impact D/A 1.7 GJ is applied to A and D and, as in experiment 1 0.85 GJ is applied to A. A can totally absorb 10.974 GJ so you would expect rigid D to bounce on A. The dynamic impact force if applied on A/D is, as stated above, simply the energy applied divided by displacement of force during impact/compression that takes a certain time. The initial impact will be followed by more impacts, if further m gets loose and drops, but energy released in each impact will be elastically and maybe plastically absorbed by intact springs. The beauty of a spring is that it can absorb energy multiple times, when loaded in succession and that this absorption takes time. The spring acts like a shock absorber transmitting energy to other springs and ground. It is very strange that NIST suggests without any evidence in its 10 000 pages 911-report that little, weak top part C (or rigid D) can apply energy on big, strong bottom part A that A cannot absorb! The figures here indicate something completely different! Why does NIST lie and spread false information to the public. Is it in order to support terrorism? It may be argued that the top 14 top springs and the 15 springs in the next layer of A below may be destroyed locally in overload by the dynamic forces at impact with D and that some extra energy released, when D and one or more loose m displace down L. The 14 top springs of A can totally absorb elastically 14 x 2.053 = 28.74 MJ and maybe plastically totally say 57 MJ and the next 15 springs about the same. The plastic destruction (failure) of springs takes time, so in the mean time the dynamic impact force (i.e. energy divided by displacement) can be absorbed elastically by intermediate springs and transmitted to ground (as a seismic wave). When one layer of springs is destroyed all m above displace down L and more energy is released - a second impact - and has to be absorbed by intact springs like a shock absorber. So D applies 850 MJ on A and about 114 MJ can be absorbed by destruction of the two top layers of springs in A and the rest is absorbed elastically by 95 other layers of springs in A and transmitted to ground. That D would destroy all 6 014 springs of bottom part A is unlikely. The springs of A will dampen the impact of D and further loose top m of A dropping, while only some local failures occur close to interface D/A. It is quite easy to verify experiment 3 in a laboratory. Just take the top C of any tower structure, compress it to a rigid block D, and drop D on the bottom part A and see what happens. Rigid D will always bounce and stop after producing some local failures at top layers with few springs of A, i.e. the weakest part of A!
Structural damage analysis experiment 4: Small top C cannot crush a bigger bottom A In experiment 4 is shown what happens, when top part C impacts bottom part A from above. Top part C is thus dropped on bottom part A from L = 3.7 m. This is the infamous WTC 1 event. 13 top floors m of WTC 1 drop on 97 intact floors/columns m below and according videos of suspect origin the 97 floors/columns below are destroyed in a fountain of smoke, dust and debris - terrible - as shown 'live on TV' September 11, 2001! In reality, of course, it cannot happen. At impact C/A 0.85GJ is applied to C (with 12 springs at bottom) and 0.85GJ is applied to A (with 14 springs at top) as explained above. However, C does not impact rigid ground as in experiment 1 and A is not impacted from above by rigid D as in experiment 3. In fact only the top m of A supported by 14 springs below and the bottom m of C supported by 12 springs above contact each other in the impact and the dynamic forces are then transmitted via the springs to other m in A and C via springs that behave elastically and dampen the impact. The impact, like in experiment 3, will be split in sub-impacts when/if further floors m gets loose and drops but energy released in each sub-impact will be elastically and plastically absorbed by the springs. So in experiment 4 the initial impact will really be dampened, i.e. takes longer time, as both A and C … and ground … will dampen (absorb the energy of) the local impact C/A. It also means that the dynamic forces are reduced. That small/weak C will crush big/stronger A at increasing speed and by gravity is impossible. That C - that can absorb much less energy elastically and plastically than A - can apply, via dynamic forces at impacts, and release, via structural/spring failures, more energy on A and destroy A is impossible: C will destroy its own springs first, before A is starting to get destroyed and then C cannot apply or release more energy to destroy A. In 3D reality there will only be some local failures at interface C/A at impact, elements of C and A then get locally entangled, friction develops and loose top part C will then just bounce on top of A. A arrests C! There is not enough energy for anything else. In 2D model world the top line will evidently just pass by the bottom line. As seen above 0.85 GJ energy is applied to 12 bottom springs in C (and to remaining 66 springs above) and 0.85 GJ energy to 14 top springs in A (and to remaining 6 000 springs below) at impact C/A. What happens if 0.065 GJ energy E is applied to one spring with stiffness k = 3 GN/m and 3.7 m length L? Answer: the spring will compress x = 0.147 m (as x² = E/k) due to the impact or 4% L. As one spring in our example can only elastically compress 1% it means that the spring plastically deforms and breaks at impact. However, our spring is not alone but supported by other springs above and below in the structure so you have to consider that. Evidently the 6 014 springs in A can easily absorb totally 0.85 GJ energy elastically (as shown in experiment 3). If the 78 springs in C can do it, is another matter (as shown in experiment 1). It is quite easy to verify experiment 4 in a laboratory. Just take the top part C of any structure, and drop it on the bottom part A and register what happens. My experience is that C always bounces on and is arrested by A, but I may be wrong. I have only tested a limited amount of towers. No smoke, dust, debris or ejections were produced though, when dropping C on A. Many people believe that scale or size of the structure or the matters, e.g. that a small model of a structure cannot crush itself but that a bigger structure can or that material matters, e.g. that a structure of brittle elements/connections will collapse but not a structure of more ductile elements/connections. However, to believe things like that is unscientific, terrorist nonsense.
Mathematical modeling The experiment 4 impact, elastic compression of springs and damping of parts can of course easily be modeled mathematically using Finite Element Methods for any size of tower springs structure/elements/connections/material. A linear spring-damper model of the form f(t) = k*x(t) + c*v(t), where x = input displacement, v = input velocity, and f(t) = output force can be developed based on test data in the time domain of the springs. The term k is the spring stiffness (N/m) and c is the viscous damping coefficient (Ns/m). With k = 3 GN/m and c= 0.3 GNs/m the tower parts A and C become flexible and will visibly deform, compress, oscillate, be damped, for several seconds after impact C/A. Plastic deformation and it's time to develop failures of a spring are more complex to model mathematically (but it can be done). That a 407 meter tower structure will explode in smoke, dust and debris, rubble being formed and collapse from top taking place in 20 seconds as shown 'live on TV' Tuesday morning 11 September 2001 in the USA is evidently not possible in reality. What was shown 'live on TV' was just a stupid movie made by disaster animators Hollywood style using computer generated images, CGI! Imagine that! The writer's attempts to crush a structure A by dropping its top C on it have, naturally, always ended up with no springs, elements or connections failing in A and C and only bouncing/arrest of C taking place. Conclusion The writer has never seen a top part C of a tower structure impacting and destroying the bottom part A due to gravity. Reason is that such destruction is physically impossible! A always arrests C. Anyone suggesting something else or shows it 'live on TV' or on below figure is a simple terrorist. Anders Björkman, M.Sc., Heiwa Co, European Agency for Safety at Sea Beausoleil, France November 12, 2012
Appendix - Comments by world famous civil engineers not agreeing with above. I have only a good university degree and 40+ years experience of steel structural design, analysis, construction, inspection, maintenance and repairs in the marine and off shore fields, where structures are subject to more severe conditions than the WTCs. I have thus discussed my 2D findings above with many world famous civil engineers that suggest that above is not applicable to WTC 1 or 2 because they were particular cases just bolted together in 3D and it wasn't the wall supports - the springs - that failed but all the bolts holding floors and walls together that sheared off floor by floor … and the whole thing really collapsed as seen live on TV. (http://www.cbsnews.com/2100-205_162-527157.html) The WTCs were some sort of houses of cards structures - with bolts though - just waiting for 30 years to be hit by a hi-jacked plane up top, catch fire and suddenly … POUFF, POUFF. These world famous civil engineers better remain un-named. I have therefore 2010 started a Challenge - the Heiwa Challenge at http://heiwaco.tripod.com/chall.htm . It is very simple. Anybody that (1) can describe a structure A with a top C and (2) show, e.g. in a laboratory, how top C crushes bottom A by gravity receives € 1 000 000:- . ---
I really looked forward to presenting above paper at Evanston 5-7 August but the EMI invitation was withdrawn July 28. If any engineer, though, finds that my conclusion is wrong, she/he has the possibility to win my €1M Challenge. Sorry I couldn't attend at Evanston!
Another interesting paper is The Late Jolt -- Re-Examining the World Trade Center Catastrophe by Ansgar Schneider and published 2017: A model of a gravity-driven collapse of a tall building has been proposed by Bazant et al. We apply this model to the collapse of the North Tower of the World Trade Center to determine the energy dissipation per storey during the collapse. Our findings are (at most) 250 MJ during the first 4.6 sec. In the time interval between 4.6 and 7.7 sec after collapse initiation we find an additional energy dissipation per storey of 2500 MJ. Because the steel columns increase in strength towards the ground this value corresponds to a value of 2000 MJ for the storeys in the aircraft impact zone. After 7.7 sec the value reduces again. These results have two possible interpretations: Mr. Ansgar Schneider has not observed that the complete top section of the North Tower of the WTC disappeared in thin air during the first 4.6 seconds!
|