|
|
|
|
SEC. 1021. AFFIRMATION OF AUTHORITY OF THE ARMED FORCES OF THE UNITED STATES TO DETAIN COVERED PERSONS PURSUANT TO THE AUTHORIZATION FOR USE OF MILITARY FORCE. (a) IN GENERAL.- Congress affirms that the authority of the President to use all necessary and appropriate force pursuant to the Authorization for Use of Military Force (Public Law 107-40; 50 U.S.C. 1541 note) includes the authority for the Armed Forces of the United States to detain covered persons (as defined in subsection (b)) pending disposition under the law of war. (b) COVERED PERSONS. - A covered person under this section is any person as follows: (1) A person who planned, authorized, committed, or aided the terrorist attacks that occurred on September 11, 2001, or harbored those responsible for those attacks. (2) A person who was a part of or substantially supported al-Qaeda, the Taliban, or associated forces that are engaged in hostilities against the United States or its coalition partners, including any person who has committed a belligerent act or has directly supported such hostilities in aid of such enemy forces. National Defense Authorization Act for Fiscal Year 2012
Hopefully below article will not make me a covered person in the eyes of the authority for the Armed Forces of the United States. |
|
A
simple structural model of WTC 1 is shown
right. It
consists of a lower part A and an
upper part C. Part
A consists of 97 horizontal elements or floors,
each with mass m (including supports just below),
stacked on top of one another with vertical support
elements, pillars and columns, in between of height
h = 3.7 meters. Part A is supported by
ground, GF. Total mass of A is 97 m! It is 358.9
meters tall. Upper
part C consists of 14 horizontal
elements/floors, each with mass m as part A,
stacked on top of each other with vertical support
elements in between of height h. Total mass of
Upper part C is 14 m. It is 51.8 meters
tall. Part
C is a continuation of part A and
initially there are also vertical support elements
between parts A and C. Purpose
of this article is to show that Upper part C cannot
one-way, progressively, floor by floor, crush down
Part A by gravity. There are
thus 111 horizontal elements/floors in the total
structure A+C. The
vertical support elements, e.g. pillars or columns,
are supposed to carry the horizontal elements above
them with a factor of safety, FoS, of 3. For
simplicity the mass of the pillars are included in
the element above. There are 280+ support elements
between any floor; only two are indicated in the
model. It
means that support pillars between GroundFloor, GF,
and 1st element can carry 111m with an FoS of 3 and
that the pillars between parts A and C can carry 14
m with a FoS of 3, &c. The support pillars
evidently get stronger the lower they are in the
structure. Support
pillars below element # 1 carries 111m, support
pillars below element # 97 carries only 15m,
&c. You could say that the lowest pillars are
abt. 8 times stronger than the pillars above
element #97. The total cross area of support
elements is much bigger at the bottom. The
easiest way to destroy parts A and C
is evidently to suddenly remove - by controlled
demolition - the strongest support pillars
of the parts, i.e. those below element #1 in bottom
of part A. Then a combined mass of 111m
drops height h 3.7 meters and hits ground. With
luck the energy applied on parts A and
C at contact with ground will then destroy
the vertical support elements below element #2
above and then a combined mass of 110m drops height
h and hits ground again. When this has been
repeated 110 times, all vertical support elements
of parts A and C are destroyed and
you have a nice pile of 111 horizontal elements on
ground. Controlled demolition always starts from
bottom/up by controlled removal of the
strongest load bearing elements down at the
bottom; then the mass above drops, hits ground
and energy is applied to the structure above, where
the next assembly of load bearing vertical support
elements are destroyed, etc, etc. Evidently you
cannot destroy part A by removing vertical load
bearing elements above it or up top! It will be
explained below: The 280+
steel supports between elements #97/98 are suddenly
removed by FIRE and part C is
supposed to drop free fall distance h due to
gravity g so that bottom of part C impacts
top of part A. Part C will not drop
sideways at impact. During
the 3.7 m drop (free fall) that takes 0.86 seconds
part A is suddenly unloaded and carries 14 m
less mass, while all supports in part C do
not carry any load at all. The
energy input E at contact C/A is E
= 14 m h g Joule and the impact velocity is
known (8.52 m/sec). At
impact between horizontal floors #97/98 of parts A
and C a big pressure load is applied on
both horizontal elements/parts. Let's
assume the two elements/parts, i.e. the floors,
intact or damaged, transmit the load to the
vertical supports. Evidently
all the vertical supports between horizontal
elements in both parts C and A then
first deform elastically absorbing energy
and part of this energy is also absorbed by the
ground but, if the compressive stress becomes too
high in an element anywhere in the structure,
that element will break. We are
of course interested to know what vertical
support elements will break first!
Intuitively
we know that the supports below horizontal element
#1 above GF will not fail first; they are the
strongest in the whole structure. Same thing for
the weakest support elements below element 111 (the
roof). They are too far away from the impact.
Intuitively we know that, if any support
elements will fail, it is either the vertical
supports between floors #96/97 of part A
below or floors #98/99 of part C
above impact. It is
interesting to note that supports between floors
#96/97 of part A before drop carried mass 15
m with an FoS 3, while the supports between floors
#98/99 of part C only carried mass 13
m. The terrorists at NIST suggest that all support elements, i.e. 111 x 280 = 31.080 pillars fail within 15 seconds in a fountain of debris, but we take it slower step by step. There are thus three possibilities to initiate destruction: i) weaker support elements of part C fail between floors #98/99 above impact, or ii) stronger support elements of part A fail between floors #96/97 below impact, or iii) no further elements fail, i.e. part C bounces on part A. Note that the supports are virtual and broken supports just disappear at no time. Let's assume, like the terrorists, that the failures initiate a second free fall drop, i.e. no bounce takes place. In case i) it will be a reduced part C of mass 13 m that drops and impacts floor #98. In case ii) it will be part C of mass 14 m + top m of part A, total 15 m, that drop and impact floor #96. At this second impact and high pressure between two elements the structure compresses elastically again and once more the question is - what support elements will break, if any? The ones below or the ones above? Or none. The ones below are getting stronger and stronger relative to any undamaged supports above. So sooner or later the weaker supports above will start to fail! In the real world the weaker supports above in a structure cannot crush the stronger supports below. The worst case is that all supports in upper part C are broken and then any crush-down is arrested, i.e most of part C simply bounces and comes to rest on part A. This is all in
accordance with the Björkman Axiom regarding
structures:
A smaller
part of an isotropic or composite 3-D structure,
when dropped on and impacting a greater part of
same structure by gravity from above, cannot
one-way crush down the greater part of the
structure. The Björkman Axiom explained The Björkman axiom can be better understood by looking at what happens when two objects C and A collide inelastically, i.e. the objects are deformed/damaged in an isolated space (in some simple, numerical examples): We start with two objects C and A of same mass (and other structural properties). Note how the velocity of the moving part C changes (is reduced) at collision! C has mass m = 1 kg and is moving at velocity v = 10 m/s and its kinetic energy (mv²/2) is 50 J and its momentum (mv) is 10 kgm/s. A has also mass 1 kg but is stationary (0 energy and momentum). After inelastic collision C with A in a closed space we assume both objects move at velocity 5 m/s - momentum 10 kgm/s is conserved - and then we observe that the kinetic energy of A+C is only 25 J. Note that moving part C slowed down from 10 to 5 m/s in this inelastic collision! Where did the 25 J go? (In an elastic collision A gets velocity 10 m/s and C becomes stationary and no energy and momentum is lost). If an inelastic collision really can take place in a closed, isolated space as suggested; mass C 1 kg/10 m/s/ 50 J/ 10 kgm/s hits stationary mass A 1 kg/0/0/0 and both (C+A) proceeds at 5 m/s (glued together?) after collision thus with constant momentum 10 kgm/s but only with 25 J kinetic energy, the missing 25 J energy evidently was transformed into, e.g. heat, deformations, failures of C and A at the inelastic collision. 12.5 J/kg kan really locally transform/modify C and/or A in many ways, but it depends on the structural properties of C and A. The difference between an elastic and inelastic collision in closed space is that, in the latter, structure is modified and kinetic energy is transformed into heat. Momentum is always conserved. Now lets study an example of the axiom. C is the smaller part and remains at 1 kg and A becomes the bigger part! Let's say that A is 9 times bigger - 9 kg - than C and that C+A (10 kg) proceeds at only 1 m/s after collision/glued together in a closed space (momentum 10 kgm/s is conserved) and that you lose 45 J in the kollision or only 4.5 J/kg on A+C together. Note that moving part C now reduces speed from 10 to 1 m/s in order to transmit energy. However, if the 45 J energy used to transform the objects is split 50/50 between C and A, then 22.5 J/kg is applied on small part C and only 2.5 J/kg is applied on big part A. Reason for this is that the contact forces between C and A are equal at contact. In this case and, if
C and A,
has same structure/properties and are subject
to identical forces, C breaks up long before A
in an inelastic collision, as small
C must absorb 9 times more energy than big
A. The axiom suggests that similar things
happens when two objects collide in an open space,
where A may be fixed to, e.g. ground, e.g.
like WTC 1 on 911. It means that you cannot
crush an isotropic or composite 3-D structure A by
a part C of itself (C = 1/9 A) by dropping part C
on A using gravity. Part C either bounces (elastic
collision) on A or gets damaged (inelastic
collision) in contact with A and is stopped by A
that is also damaged a little. It is quite basic
and all due to forces/energy applied and that the
two parts have identical structure. Materials, size
and particulars of the elements of the structure A
doesn't matter the least. Part C of A cannot
destroy A, as C must absorb much more energy per
mass unit than A in the inelastic
collision. Thus no structures, 1,
2 or 5 meters tall, or 100, 200 or 500 meters tall
exist that will one-way crush down, when a small
part C is dropped on the remainder part
A. In the real world 280+ support
columns cannot fail simultanesouly due to
FIRE, so no section C can drop
vertically for a perfect impact. The above
processes can evidently be studied in a model at
smaller scale! However, one difficulty is that most
structures can elastically absorb
>10.000
J energy per kilogram structure so you have to
chose a a very weak structure to get going.
Regardless, the smaller part is always destroyed
first at the collision. First impact! Upper part C shall contact lower Part A at velocity 8.5 m/s corresponding to a drop of 3.7 m. This can be done i) by a drop of 3.7 m, or ii) by accelerating part C from shorter distance using, e.g. a spring, &c. In the latter case we can turn the model 90° and apply a force on part C and shoot C on A and see what happens at different velocities (up to max 8.5 m/s) as per figure below, where it is also indicated that the supports between floors are getting bigger at the bottom (left) of the structure. At contact C/A (lower figure) the force is evidently transmitted to part A and ground and parts C and A are deformed ... and maybe local failures occur! 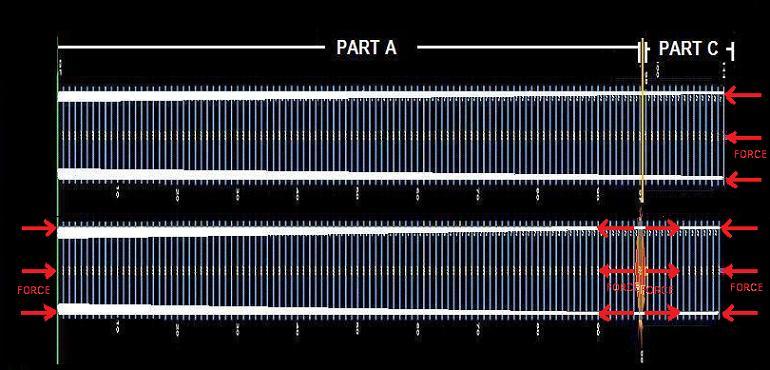 Deformations and local Failures After impact deformation and maybe failures of parts C and A take place. Using method i) above we can study what deformation and failures takes place incl. effects of gravity. Using method ii) above we just study the deformation and failures due to impact excl. effects of gravity.
Second Drop/second Impact/Crush-down (or complete Compression of part A)? When you have overcome the problem of deformation and first failures after impact, you evidently must ensure that part C can continue to impact/deform/damage part A due to gravity and produce progressive collapse crush-down. So the model must be upright again or you reload the spring and shoot/apply a new force on modified C towards modified A in the horizontal position to simulate gravity. With experience gained from small scale models you will soon find that small part C cannot destroy big part A in any position. Only terrorists and supporters of terrorism believe otherwise This is all in
accordance with the Björkman Axiom regarding
structures:
A smaller
part of an isotropic or composite 3-D structure,
when dropped on and impacting a greater part of
same structure by gravity from above, cannot
one-way crush down the greater part of the
structure. (PS - WTC1&2 were destroyed from bottom up on 9/11/01. What you saw live on TV was just an animation of computer generated images produced by the real terrorists assisted by Hollywood to make you believe the Usama Bin Laden planes/fires up top produced the destruction of the (empty) towers).
|