3.2 Externa krafter på visiret
Externa, yttre, vågkrafter angriper visiret i sjögång, när visiret doppas ner under vatten, 1.19. Visiret sitter utanför överbyggnaden, dvs vågkrafterna angriper en lös del förbunden med överbyggnaden via fem olika fästpunkter.
Slutrapporten (5) simulerar den totala belastningen (Z-kraften) på 'Estonia's visir. Simuleringen (blå i Figur 12.7 i (5)) anger att det tar 800 timmar (!) innan en uppåtriktad Z-kraft överstiger >6 MN (600 tons) i sjögång som rådde vid olyckan (Beaufort 7 med 4,3 meters vågor)! Denna simulering är en förfalskning - naturligtvis uppträder inte krafter av denna storleksordning på en lös del fastsatt i överbyggnaden. Nedan skall visas hur förfalskningen utförts:
Den simulerade Z-kraften på visiret är enligt slutrapporten (5) (sid 157) en kombination av
(a) visirets vikt,(b) visirets tröghetskraft,
(c) flytkraften som verkar på visiret,
(d) hydrodynamiska krafter (added mass och dämpning) på visiret,
(e) Froude-Krylov kraften,
(f) vattenströmningskrafter runt det nersänkta visiret, och
(g) den icke-linjära vertikala stötkraften (sic), som angriper en del av visiret under kort tid - när/om det slår emot vattenytan.
De yttre krafterna kan aldrig lyfta visiret
Vikten (a) är en kraft neråt hela tiden - säg 55 ton för 'Estonia'.
Tröghetskrafterna (b) verkar upp/ner med stampningen och är en funktion av accelerationen, men eftersom den är liten - max 0,2-0.3 g (g=9.81 m/s²) spelar de inte stor roll - tröghetskraften är i ordningen 10-20 ton.
Den huvudsakliga vertikala, uppriktade kraften är
flytkraften (c), när visiret är nersänkt under vågorna. Den är en funktion av visirets volym (cirka 165 m3 till övre däck åtta meter över vattenlinjen för 'Estonia'). Men 'Estonia's visir är två meter över vattenlinjen och sällan nersänkt mer än fyra, fem meter och då är flytkraften upp bara 40-50 ton under ett par sekunder. Sedan har vi de
hydrodynamiska krafterna (d) som beror på nersäkningshastighet och dämpning när visiret kommer under vatten. De är också små - säg 30% av (c). Froude-Krylov kraften (e) och vattenströmningskrafterna runt det nersänkta visiret (f) är även de små. Totala kraften (a) till (f) är därför liten, när visiret är under vatten under kort tid, säg 2 sekunder, vikt och tröghetskraft balanseras av flytkraften.
I Beaufort 7 med 4,3 meters vågor överstiger knappast flytkraften vikten, dvs visiret rör sig inte uppåt alls! Totalkraften på visiret (uppåtriktade vågkrafter minus visirets vikt) är i stort sett noll. Så hur kan kraften plötsligt bli >600 ton?
Den icke-linjära vertikala stötkraften
Sedan är det ytterligare en kraft som verkar på visiret - den icke-linjära vertikala stötkraften (g). Den är ytterst kortvarig och beror på färjans fart och kurs vis-à-vis vågorna och visirets form och vinkel mot havsytan. Kommissionen anger (utan bevis naturligtvis) att denna stötkraft är 700-1.000 ton i det givna vädret och verkar under några millisekunder - och att det var den kraft som slet bort visiret från överbyggnaden Appendix 2. Det finns inga kända metoder att simulera på ett visir! Så hur gick förfalskningen till?
Modellprov och simulering
Kommissionen anger att modellprov kan användas för att beräkna fullskalekrafter och -moment på visiret.
Författaren känner inte till någon metod att extrapolera en kraft eller moment mätt på ett visir i modell till full skala. Kommissionens uppgifter här är alla förfalskningar!
De olika kraftkomponenterna (a), (b), (c), (d), (e), (f) och (g) följer olika skalfaktorer/regler och är svåra att mäta separat. Ett lokalt tryck på en yta i modell kan å andra sidan skalas upp. Men i Kommissionens modellprov utförda av SSPA Marin AB mättes bara totalkraften på ett upphängt visir. Den kan inte skalas upp enligt kända regler. Kommissionen anger vidare att alla olika kraftkomponenter (a), (b), (c), (d), (e), (f) och (g) kan beräknas teoretiskt - simuleras - medan författaren inte känner till några sådana erkända metoder. Kommissionens uppgifter är 100% lögnaktiga, felaktiga och vilseledande!
Otroligt anger sedan Kommissionen i slutrapporten (5) kapitel 12.1 och 12.2 att fullskalekrafter på 'Estonia's visir extrapolerade från modellprov jämförs väl med samma krafter beräknade,simulerade, teoretiskt. Det låter bra, men det saknas vetenskapliga belägg för saken.
Både modellprov och teoretiska simulationer av Kommissionen är manipulationer/påhitt utan vetenskaplig bakgrund. Ren lögn alltihop, lätt att visa.
Belastningen på visiret överförs till överbyggnaden
Den huvudsakliga vertikalkraften (uppåt) är en flytkraft som funktion av visirets nersänkta volym under vattenlinjen (maximalt ca 165 m3 under back/väderdäcket, om visiret är 8 meter (!) under vattenlinjen, vilket är mycket osannolikt) och nersänkningshastigheten. En annan vertikalkraft är, som nämnts, en kortvarig stötkraft, som kan uppträda, om visiret smäller i havsytan. Den kraften beror på fartygets kurs och fart, vinkeln mellan visir och vattenlinje och visirets form, och vädret/våghöjden.
Klassningssällskapen anser att man skall räkna med en total vertikalbelastning, som är en funktion av visirets horisontalt projicerade yta gånger ett hypotetisk yttre vattentryck, som i 'Estonia's fall skulle vara cirka 8-9 ton/m², minus visirets vikt. Bakgrunden till den beräkningsmetoden är ingenjörsmässig, dvs erfarenhetsunderbyggd 3.6. Den metoden ger mycket stora konstruktionsbelastningar.
Den uppåtriktade kraften på visiret kan enbart överföras till överbyggnaden via de tre låsen. Vi bortser från att låsen pressar visiret akterut mot de vertikala gummipackningarna och att en betydande del av den yttre kraften överförs till överbyggnaden via friktion i den vertikala tätningen.
|
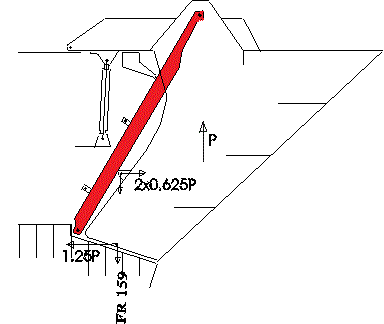
Om vi antar att den uppåtriktade flytkraftens centrum är cirka 2.5 m framför låsen och det vertikala avståndet mellan sido- och Atlantlås är 2.0 m, är det lätt att visa en vertikal kraft P på visiret (flytkraft minus visirets vikt) överförs till låsen som en horisontal tryckkraft 0.625*P i varje sidolås och som en horisontal dragkraft 1.25*P i Atlantlåset. Se figur 3.2. En uppåtriktad kraft på visiret kommer alltid att trycka in sidolåsen och dra ut Atlantlåset. Därför var sidolåsens visiröglor alltid under tryck, medan Atlantlåsets visirögla var under dragpåkänning. Det framgår också av bilder av de slitna låsen. Beroende på glapp i låsen och gångjärnen kunde en viss del av den uppåtriktade kraften överföras till överbyggnaden via gångjärnen på däck. Emellertid, ur rent praktisk synvinkel var gångjärnens enda funktion att öppna/stänga visiret. Då uppträder stora böj- och skjuvkrafter i varje gångjärnsarm och reaktionskrafter i själva gångjärnsörona på däck. --- |
|